Project desert tortoise
Problem Statement
I found an embedded data stream in the NOAA DSB broadcasts that contains doppler data from ground-based transmitters. These messages contain short bits of data (up to 64 bytes) and the time vs frequency data required to geolocate them to a km or so (in theory). My friends at the hackerspace kept making jokes about using to find a desert tortoise with a huge transmitter glued to its back, and thus the project name was born...
Work
Doppler Model
The model is complex enough to need its own page... [1]
Time
DCS/2 (NOAA-15 and NOAA-18) appear to have less precise hardware than ADCS (NOAA-19). No correction factor seems needed for ADCS, but one is needed for DCS/2 spacecraft For example:
TXID:FB3AD000 SPID:NOAA-19 ADCS ID Local Time ADCS Time Freq LTdelta STdelta 196 111.7084 10060.62 -89901.75000 50.0525 **50.00 414 161.7609 10110.62 -93257.56250 49.9911 **50.00 611 211.7520 10160.62 -97425.96875 49.9558 **50.00 838 261.7078 10210.62 -101951.8438 50.531 **50.00 1030 312.2388 10260.62 -106160.9063 99.4706 **100.00 1402 411.7094 10360.62 -112104.6875 50.0451 **50.00 1582 461.7545 10410.62 -113888.6563 50.0914 **50.00 1755 511.8459 10460.62 -115123.4375
TXID:FB3AD000 SPID:NOAA-18 DCS/2 Raw, and with Correction Factor of 0.95494 ID LTime Stime SDT CSTime SCDT LDT 117 169.1584 5066.25 *104.71 4837.964775 99.99177 99.9318 391 269.0902 5170.96 *52.36 4937.956542 50.00066 50.1962 586 319.2864 5223.32 *52.36 4987.957201 50.00066 49.8038 757 369.0902 5275.68 *104.7 5037.957859 99.98222 99.9971 1110 469.0873 5380.38 *52.37 5137.940077 50.01021 50.0827 1276 519.1700 5432.75 *52.36 5187.950285 50.00066 50.0039 1427 569.1739 5485.11 5237.950943
TXID:FB3AD000 SPID:NOAA-15 DCS/2 Raw, and with Correction Factor of 0.95494 ID LTime Stime SDT CSTime SCDT LDT 418 281.9768 12293.59 52.35 11739.64083 49.991109 50.0000 576 331.9768 12345.94 52.37 11789.63194 50.0102078 50.0000 728 381.9768 12398.31 52.36 11839.64215 50.0006584 50.0000 886 431.9768 12450.67 52.33 11889.64281 49.9720102 50.0356 1025 482.0124 12503.00 52.36 11939.61482 50.0006584 49.9644 1163 531.9768 12555.36 11989.61548
Orbital Determination
In order to correlate the doppler shifts to geo-locations we need to know the position of the spacecraft at each moment. Matlab does not have readily available tools to do this, so I wrote a quick python script using pyephem which one can query directly from matlab or interface with directly. When given a UTC time and date, the script will spit out instantaneous lat/lon of the satellite as well as orbital period, inclination, and altitude/radius. We will use all of these parameters to initialize and optimize our doppler model.
#!/usr/bin/env python
import time
import datetime
import ephem
import optparse
import sys
parser = optparse.OptionParser()
parser.add_option("-t", "--timestamp", dest="timestamp",
help="Date and time to look for stuffs",
metavar="TIMESTAMP")
parser.add_option("-l", "--lattitude", action="store_const", dest="mode", const=1,
help="ONLY return the lattitude at datetime",
)
parser.add_option("-o", "--longitude", action="store_const", dest="mode", const=2,
help="ONLY return the longitude at datetime",
)
parser.add_option("-r", "--radius", action="store_const", dest="mode", const=3,
help="ONLY return the radius of the spacecraft at the datetime",
)
parser.add_option("-a", "--altitude", action="store_const", dest="mode", const=4,
help="ONLY return the altitude of the spacecraft above sealevel at the datetime",
)
parser.add_option("-p", "--period", action="store_const", dest="mode", const=5,
help="ONLY return the orbital period of the spacecraft",
)
parser.add_option("-i", "--inclination", action="store_const", dest="mode", const=6,
help="ONLY return the inclination of the spacecraft",
)
options,args = parser.parse_args()
if options.timestamp:
# Try parsing the date argument
try:
timestamp = datetime.datetime.strptime(options.timestamp, "%Y-%m-%d %H:%M:%S.%f")
except:
print "Error parsing date input:",sys.exc_info()
sys.exit(1)
#example TLE name ./TLE/noaa2016-02-14.txt
filename = "noaa" + datetime.datetime.strftime(timestamp, "%Y-%m-%d") + ".txt"
try:
fo = open("/home/pi/pyephem/TLE/" + filename, "r")
except:
print "TLE file not available for this date :(<br>"
print filename
sys.exit(1)
line = fo.readline()
while line != "":
if "NOAA 18" in line:
line1=line
line2=fo.readline()
line3=fo.readline()
break
line = fo.readline()
fo.close
NOAA = ephem.readtle(line1, line2, line3)
NOAA.compute(timestamp)
pi = 3.14159265359;
if options.mode == 1:
print('%f' % ((180.0/pi)*NOAA.sublat))
elif options.mode == 2:
print('%f' % ((180.0/pi)*NOAA.sublong))
elif options.mode == 3:
print('%f' % (6378 + NOAA.elevation/1000))
elif options.mode == 4:
print('%f' % (NOAA.elevation/1000))
elif options.mode == 5:
print('%f' % (86164.0 / float(line3.split()[7])))
elif options.mode == 6:
print('%f' % (float(line3.split()[2])))
else:
print('%f %f %f' % ((180.0/pi)*NOAA.sublat, (180.0/pi)*NOAA.sublong, NOAA.elevation/1000))
Doppler Data
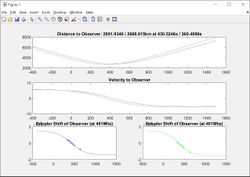
Doppler shifts produce sigmoid functions, so we should see a very specific shape with an inflection point where the satellite passes overhead and relative velocity reaches zero, then reverses. The last three bytes hold the key. Some good data I have comes from a Baltic sea area transmitter (fishing ship? sea float?) with the ID 0x24000530. By analyzing the bytes, we can figure out how to combine these three bytes to produce the frequency as received by the spacecraft.
Latest Doppler Shift Model for Geolocating ARGOS Transmitters
A matlab script that interfaces with an updated version of the above python script has been created that does pretty much all of the hard work for you. You must provide Spacecraft ID (15, 18, 19) T0 time and date of the time axis, and the time and frequency data. There is a function to fine tune the orbital period and and satellite radius to minimize the error directly at the frequency inflection point by providing a fudge factor for each (which is different for every solution set). This script will attempt to find the best position and spit out the latitude and longitude. Be aware that there are always TWO possible solutions, and they become more and more fuzzy the fewer the data points you feed it. Multiple satellite passes are required to discern which location is the correct one!
http://wiki.nebarnix.com/wiki/File:Doppler3DRotationInclination3FitandWebephem.m
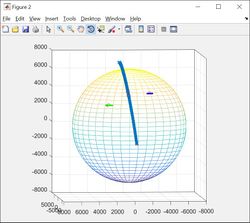
Result 1 Nov 2015
Results are shown below, the plotted points represent the solutions from two passes 20 minutes apart (NOAA15 and NOAA18). The distantly spaced models uses the 3 DOF model which assume a doppler scaling of 1.0 (just trust the raw frequency data) whereas the more closely spaced data uses the 4 DOF model that solves for slight errors of the curves (but where are the errors coming from? Ionisphere? spacecraft calibration?). Both models solve for frequency offsets of the transmitter.

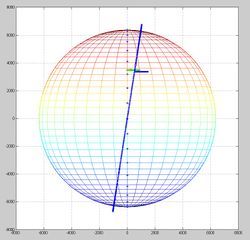

Updated results 11 Nov 2015
I learned that geocentric latitude (what the model and ephemris uses) is NOT the same as geodetic latitude, which is what google maps uses (which is because the earth is an oblate spheroid). The (simplest) formula to convert is (it gets more complex as you start getting super accurate, like the WGS84 datum that your GPS uses)
GeodLat = atand(tand(GeoCentricLat)/(1-0.00666667))
When you correct for the difference it shifts everything north by about 20 arcminutes.....
Result 2 Feb 2016
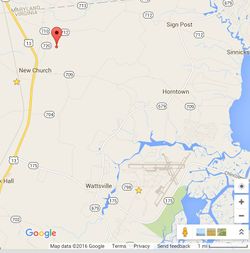
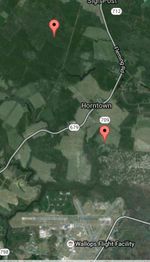
First discovery of actual location of transmitter occured while driving along Chincoteague road by the NOAA facility on the NASA Wallops base. The decoded bits show an ID 01D81000, which was found in in the embedded telemetry DCS stream. I used this to fine-tune my model, also this is the first test to use WGS95 elliptical earth model.
List of Discovered Transmitters
68961013 - NASA Goddard, Maryland, or in the area.
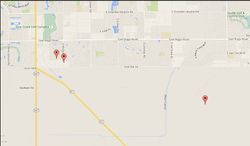
01B90000 - NASA Goldstone, around (35.335948, -116.806606)
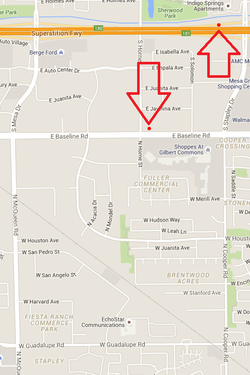
FB3AD000 - Telonics, Mesa, AZ (33.384355, -111.811219)
01D81000 - NASA Wallops NESDIS (37.94648, -75.46059)