Cheap Educational Scope
Problem Statement
I needed a quick idea for summer camp educational workshop that was 'sciencey'. I remembered seeing this thingiverse link a while back and sharing it with a friend of mine who is an elementary school teacher. I wanted to do this as a workshop but also to understand the operation behind it as I am ashamed to say that my knowledge of optics is pretty bad...
I also wanted to understand the weak spots of the scope so that older kids could make a more advanced version that would be more capable or easier to use.
The Eye
I first used ray tracing theory to understand the real and virtual image locations. I was hung up very quickly on the fact that without an eye, a virtual image is pretty useless. The eye is an integral part of a microscope!!!
Luckily I found some information on the human eye. Some of the really important ones are
- Visual acuity: 2 arcminutes
- Distance of Nearest Distinct Vision: 25cm (between this and infinity are good places to place your final virtual image)
- Translated visual acuity at the distance of nearest distinct vision: 145µm (wow, my eyes are amazing!!)
Reminder to myself to scan and stick in the raytrace model
The Cameras
Walmart! 33mm focal length lenses. Full lens diameter not usable, need to stop down with a 3mm stop.
The 2-lens Matlab Model
Remember - Optical magnification and apparent magnification and perceptual magnification (I totally made up that term) are very different things.
- Optical Magnification - The ratio of object to image.
- Apparent Magnification - Takes into account the fact a detector will see angles, therefore, distances from the detector matter. This is the ratio of the angular size of the object placed at area of nearest focus (nearest distinct vision in humans, different for a camera) to the angular size of the virtual image at *it's distance.
- Perceptual magnification - Same as apparent but uses the eye to object distance such that if you could put the instrument up to one eye and see it without the instrument through the other eye, even if the object is too close to focus on. Personally, this one makes the most sense.
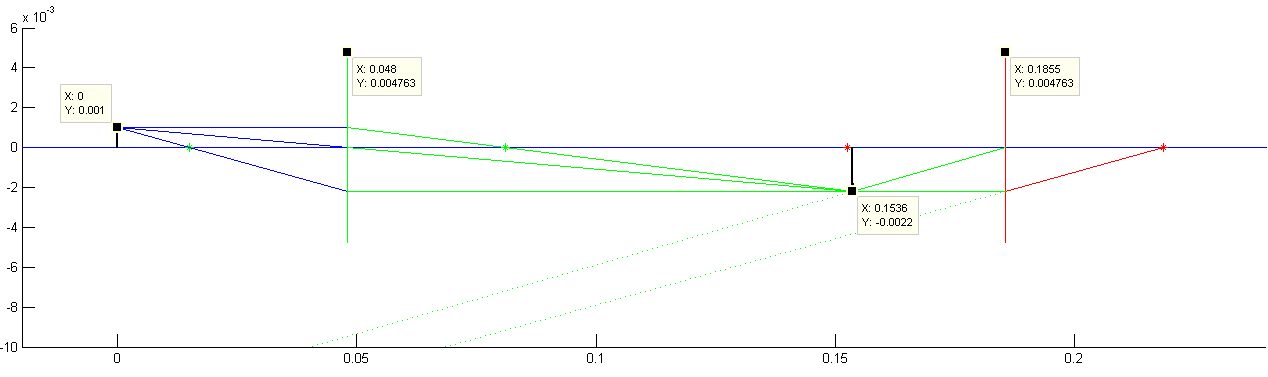
The following script is a work in progress. It produces the following figure which could be a lot better but its what I have right now.
clear; clc; %% define all constants %all units are in meters %eye relief assumed to be zero Fo=.033; %objective focal length Fe=.033; %eyepiece focal length Pe = .003; %entrance pupil of 3mm (refine this to include mag effect) Dndv = .25; %.25 is the distance of "nearest distinct vision" in humans Dvi = 1; %distance to final virtual image (between inf and Dndv) Aacuitydegrees = 2/60; %human visual foveal acuity is 2 arcminutes Wgreen = 550e-9; %wavelength of green light is 550nm %% Find image/object distances and magnigication of the objective lens Di = 3.2*Fo; %random guess of 4 times (iterative solution) %M=f/(f-Do) for distance to the object (thin lens & def of magnification) %M = -Di/Do %M = (f-Di)/f for distance to the image Mo = (Fo-Di)/Fo; Do = -Di/Mo; %% Find iimage/object distances and magnigication of the eye lens %Thin lens equation. Dndv is a virtual image, so it is negative. Devi = 1/(1/Fo - 1/(-Dvi)); %Total length = Obj<->image<->Eyepiece = Obj2image + Image2eyepiece Lt=Di+Devi Me = 1+Dvi/Fe; %% Find the optical and apparent magnification of the system Mt = Mo*Me %Optical (virtual size to image size) %Apparent (Different in what you can see naked eye vs magnified) %The angular size at DNVD vs the object you see through the eyepice at Dvi %This varies from person to person depending on DNDV Ma = atand((Mt*.001)/Dvi)/atand(.001/Dndv) %perceptual (difference in what you see without moving your head) %The angualr size without optics vs with optics. %Note that you probably can't focus this close so the object would be blurry %This does not vary between individuals Mp = atand((Mt*.001)/Dvi)/atand(.001/(Do+Lt)) %% Find the resolution of the system (and the max practical magnification) Theta = atand((0.5*Pe) / Do); NA = sind(Theta); Resolution = Wgreen/(2*NA); %green light resolution Dsep = 2*sind(Aacuitydegrees/2)*Dvi; %lowest resolveable distance at Dndv Moptimal = (2*NA*Dsep)/Wgreen %550nm is green light % Plot the system %% Draw the lenses Hoo = 1e-3; %height of the objective object Hoi=Hoo*Mo; %height of the objective image Hei=Hoi*Me; %height of eyepiece image Hol = (9.525e-3)/2; %height of the objective lens (radius) Hel = (9.525e-3)/2; %height of the eyepiece lens (radius) clf; hold on; axis([-.02 .24 -.01 .006]); line([-1 .3],[0 0]); %axis line([Do Do],[-Hol Hol],'Color','Green'); %objective lens plot([Do-Fo Do+Fo],[0 0],'*g'); %focal points line([Do+Lt Do+Lt],[-Hel Hel],'Color','Red'); %eyepiece lens plot([Lt+Do-Fe Lt+Do+Fe],[0 0],'*r'); %focal points %% Draw the images draw_arrow([0 0],[0 Hoo],0.5); %initial object draw_arrow([Do+Di 0],[Do+Di Hoi],0.5); %objective image draw_arrow([Do+Lt-Dvi 0],[Do+Lt-Dvi Hei],0.5); %objective image %axis([-.08 .22 -.02 .0075]); %% Draw the First lens rays line([0 Do],[Hoo Hoo],'Color','Blue'); line([Do Do+Di],[Hoo Hoi],'Color','Green'); line([0 Do],[Hoo 0],'Color','Blue'); line([Do Do+Di],[0 Hoi],'Color','Green'); line([0 Do],[Hoo Hoi],'Color','Blue'); line([Do Do+Di],[Hoi Hoi],'Color','Green'); %% Draw the Second lens rays line([Do+Di Do+Lt],[Hoi Hoi],'Color','Green'); line([Do+Lt Do+Lt+Fe],[Hoi 0],'Color','Red'); line([Do+Di Do+Lt],[Hoi 0],'Color','Green'); %line([Do+Lt Do+Lt-Dndv],[0 Hei],'Color','Green','LineStyle',':'); %virtual rays %line([Do+Lt+Fe Do+Lt-Dndv],[0 Hei],'Color','Green','LineStyle',':'); %virtual rays line([Do+Lt Do+Lt-Dvi],[Hoi Hei],'Color','Green','LineStyle',':'); %virtual rays line([Do+Di Do+Lt-Dvi],[Hoi Hei],'Color','Green','LineStyle',':'); %virtual rays %axis auto;
RESULTS ----------------------------- Do = 48mm (object-lens distance for an in focus image) Devi = 31.9mm (Eye-lens to real image distance for virtual image at 1 meter) Lt = 137.5mm (optical tube length, Do + Devi) Moptimal = 66.1 (converted to optical so you can compare against Mt for sanity check) Mt = -68.9 (optical magnification) Ma = -17.2 (apparent magnification) Mp = -12.8 (perceptual magnification)
2013 Jasper Nance KE7PHI
- I don't believe in the word "its" unless it refers to plural neuters.