Difference between revisions of "NOAA POES TIP Demodulation"
(Added time and pyephem data) |
|||
| Line 51: | Line 51: | ||
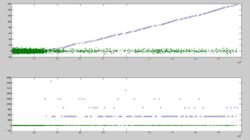
[[Image:POES_parity_errors.PNG|left|450px|thumb|A plot of parity errors vs minor frame count. Some nice large error free major frames! (NOAA-15)]] | [[Image:POES_parity_errors.PNG|left|450px|thumb|A plot of parity errors vs minor frame count. Some nice large error free major frames! (NOAA-15)]] | ||
<br clear="both"/> | <br clear="both"/> | ||
| + | |||
| + | ===Embedded Time, Date, Spacecraft ID=== | ||
| + | Each major frame contains a day number as well as day seconds and milliseconds. This can be easily converted into a time and date. | ||
| + | The matlab script spits out the following example (and notes where errors might be happening as I am currently ignoring the parity checks) | ||
| + | It also gives you a local time reference mapping relative time to absolute time. | ||
| + | |||
| + | <pre> | ||
| + | 46.6725 Local Seconds is 55986.685 Spacecraft Day Seconds which is 15:33:6.685 | ||
| + | 78.6725 Local Seconds is 56018.685 Spacecraft Day Seconds which is 15:33:38.685 | ||
| + | 142.6755 Local Seconds is 56082.685 Spacecraft Day Seconds which is 15:34:42.685 | ||
| + | 174.6755 Local Seconds is 56114.685 Spacecraft Day Seconds which is 15:35:14.685 | ||
| + | 206.6755 Local Seconds is 56146.685 Spacecraft Day Seconds which is 15:35:46.685 | ||
| + | 238.6755 Local Seconds is 56178.685 Spacecraft Day Seconds which is 15:36:18.685 | ||
| + | 239.4755 Local Seconds is 39452.805 Spacecraft Day Seconds which is 10:57:32.805 ...but this might be an error | ||
| + | 270.6755 Local Seconds is 56210.685 Spacecraft Day Seconds which is 15:36:50.685 | ||
| + | 302.6755 Local Seconds is 56242.685 Spacecraft Day Seconds which is 15:37:22.685 | ||
| + | 334.6755 Local Seconds is 56274.685 Spacecraft Day Seconds which is 15:37:54.685 | ||
| + | 366.6755 Local Seconds is 56306.685 Spacecraft Day Seconds which is 15:38:26.685 | ||
| + | 398.6755 Local Seconds is 56338.685 Spacecraft Day Seconds which is 15:38:58.685 | ||
| + | Spacecraft: 8=>NOAA-15 | ||
| + | Day: 249 | ||
| + | </pre> | ||
===SEM-2=== | ===SEM-2=== | ||
| Line 169: | Line 191: | ||
Byte N-1 Unsure. Perhaps RSSI?<br /> | Byte N-1 Unsure. Perhaps RSSI?<br /> | ||
Byte N Also could be RSSI, also could be 2 values split into 2 12-bit numbers. Also CRC? CRC16?<br /> | Byte N Also could be RSSI, also could be 2 values split into 2 12-bit numbers. Also CRC? CRC16?<br /> | ||
| + | |||
| + | ====Orbital Determination==== | ||
| + | In order to correlate the doppler shifts to geo-locations we need to know the position of the spacecraft at each moment. Matlab does not have readily available tools to do this, so I wrote a quick python script using pyephem. Its quick, dirty, and a very rough draft. | ||
| + | |||
| + | <pre> | ||
| + | #!/usr/bin/env python | ||
| + | |||
| + | #NOAA 15 | ||
| + | #1 25338U 98030A 15273.50150732 .00000073 00000-0 49665-4 0 9996 | ||
| + | #2 25338 98.7779 272.2357 0009845 218.3502 141.6978 14.25663704903843 | ||
| + | |||
| + | |||
| + | import ephem | ||
| + | line1 = "NOAA-15" | ||
| + | line2 = "1 25338U 98030A 15273.50150732 .00000073 00000-0 49665-4 0 9996" | ||
| + | line3 = "2 25338 98.7779 272.2357 0009845 218.3502 141.6978 14.25663704903843" | ||
| + | NOAA15 = ephem.readtle(line1, line2, line3) | ||
| + | NOAA15.compute('2015/9/6 15:38:58.685') | ||
| + | #NOAA15.compute('2015/9/6 15:33:6.685') | ||
| + | #NOAA15.compute('2015/9/6') | ||
| + | print('%s %s' % (NOAA15.sublat, NOAA15.sublong)) | ||
| + | </pre> | ||
| + | |||
| + | The (painfully manually entered dates and times) come out as latitudes and longitudes looks like this when you replace the :'s with degrees and minutes symbols, which corresponds to the major frame times which I added manually. Between these points, a linear interpolation will suffice for a first cut at plotting DCS idents. | ||
| + | |||
| + | <pre> | ||
| + | Local Seconds Lat Lon | ||
| + | 046.6725 43°21'31.6 21°17'02.6 | ||
| + | 078.6725 45°12'57.1 20°35'2.8 | ||
| + | 142.6755 48°55'13.7 19°03'51.1 | ||
| + | 174.6755 50°46'1.6 18°13'57.4 | ||
| + | 206.6755 52°36'33 17°20'37.5 | ||
| + | 238.6755 54°26'45.4 16°23'19.0 | ||
| + | 270.6755 56°16'35.8 15°21'23.1 | ||
| + | 302.6755 58°06'0.1 14°14'2.5 | ||
| + | 334.6755 59°54'53.8 13°00'19.1 | ||
| + | 366.6755 61:43:10.7 11:39:1.0 | ||
| + | 398.6755 63:30:43.6 10:08:37.7 | ||
| + | </pre> | ||
| + | |||
==Todo== | ==Todo== | ||
Revision as of 10:15, 30 September 2015
Problem Statement
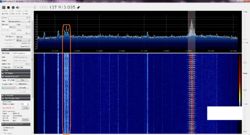
While listening to NOAA APT signals I noticed a strange telemetry signal at 137.35 and 137.77 that tracked NOAA POES sats. At first I thought it was a second sat, but then I realized that the doppler shifts matched too closely. I found the handbook for the satellite constellation, which makes mention of a DBD or TIM signal
Research
I can't actually find any instance of anyone using SDR to decode this signal. I decided that this needed to change :)
I found these documents which describe the modulation and format [1] [2]
Modulation Format
I discovered that this is a very old modulation scheme, dating back to at least the late 60's. The scheme is a BPSK that uses a modulation index of 67 degrees to preserves the carrier for tracking purposes. It is also Manchester encoded, which means that even though the stream is 8320 bps, it is encoded using double the number of symbols, or 16,640 sps.
GNU Radio Script
I wrote a GNU radio workflow to prepare the data for demodulation. http://nebarnix.com/sdr/nocarrier_lowpass_polyphase_equalizer.grc
File Source->Throttle->AGC2->Carrier Tracking PLL->High Pass Filter (to remove carrier)->Polyphase Clock Sync w/ lowpass proto->CMA Equalizer->File Sink (post GNU radio file and block image here)
Matlab Script
I decided to process the data in Matlab because I wanted access to all of the analytical tools until I could figure out what I was doing. Update: added some updates to the Manchester decoder. Here's a link to the crappy matlab script I have written to do most of the data processing and extraction.
http://wiki.nebarnix.com/w/images/6/69/Decode_syncd_IQ2.m
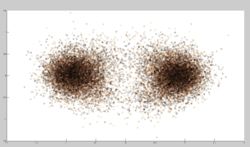
Here's the final constellation of bits. It is still crappy.
The circles are the locations where the sync word, "11101101 1110001 0000" appear. The bottom plot is a diff of the first, showing intervals of 832bits (minor frame length) which proves this is good data. The green dots are where there are Manchester encoding errors (two 1's or two 0's in a row not on a bit boundary). Note that there is no error correct -- unless I find a better way to clean up the phase constellation (or get a better signal) -- or weed out 'barely' bad bits, I probably don't have more than a couple perfect minor frames... it takes 32 seconds or 3200 minor frames to make up a whole major frame. I have some work left to do smile emoticon
Raw IQ Recordings
- http://nebarnix.com/sdr/POES_56k250.raw 56.250khz IEEE 32-bit float raw IQ recording of the (I think) NOAA-18 beacon at 137.35Mhz
- http://nebarnix.com/sdr/pll_nocarrier_polyphased_equalized_loproto.raw IEEE 32-bit float raw IQ output from the GNU radio script at 1 symbol per sample to pull into matlab.
- http://nebarnix.com/sdr/pll_nocarrier_polyphased_equalized_loproto4.raw IEEE 32-bit float raw IQ output from the GNU radio script at 1 symbol per sample to pull into matlab. Best recording to date, from reddit user _COD32_. NOAA-15.
Data Extraction and Validation
I have updated the matlab script to extract a few of the instruments embedded in the stream! First, there is a parity byte in each minor frame that splits the frame into 6 chunks and checks each chunk for errors. One could in theory zero out or at least flag questionable chunks when plotting to more easily spot bad points.
Embedded Time, Date, Spacecraft ID
Each major frame contains a day number as well as day seconds and milliseconds. This can be easily converted into a time and date. The matlab script spits out the following example (and notes where errors might be happening as I am currently ignoring the parity checks) It also gives you a local time reference mapping relative time to absolute time.
46.6725 Local Seconds is 55986.685 Spacecraft Day Seconds which is 15:33:6.685 78.6725 Local Seconds is 56018.685 Spacecraft Day Seconds which is 15:33:38.685 142.6755 Local Seconds is 56082.685 Spacecraft Day Seconds which is 15:34:42.685 174.6755 Local Seconds is 56114.685 Spacecraft Day Seconds which is 15:35:14.685 206.6755 Local Seconds is 56146.685 Spacecraft Day Seconds which is 15:35:46.685 238.6755 Local Seconds is 56178.685 Spacecraft Day Seconds which is 15:36:18.685 239.4755 Local Seconds is 39452.805 Spacecraft Day Seconds which is 10:57:32.805 ...but this might be an error 270.6755 Local Seconds is 56210.685 Spacecraft Day Seconds which is 15:36:50.685 302.6755 Local Seconds is 56242.685 Spacecraft Day Seconds which is 15:37:22.685 334.6755 Local Seconds is 56274.685 Spacecraft Day Seconds which is 15:37:54.685 366.6755 Local Seconds is 56306.685 Spacecraft Day Seconds which is 15:38:26.685 398.6755 Local Seconds is 56338.685 Spacecraft Day Seconds which is 15:38:58.685 Spacecraft: 8=>NOAA-15 Day: 249
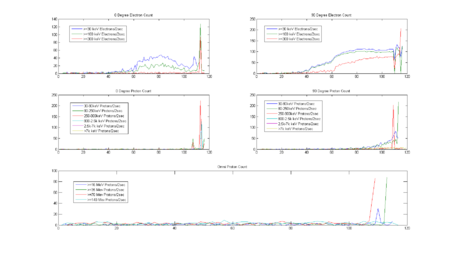
SEM-2
The SEM-2 (Space Environment Monitor) contains two experiments, the MEPED (Medium Energy Proton and Electron Detector) and the TED (Total Energy Detector) The following MEPED and TED data was taken as the NOAA15 spacecraft flew north from Hungary to Scandinavia and into the auroral oval.
DCS-2
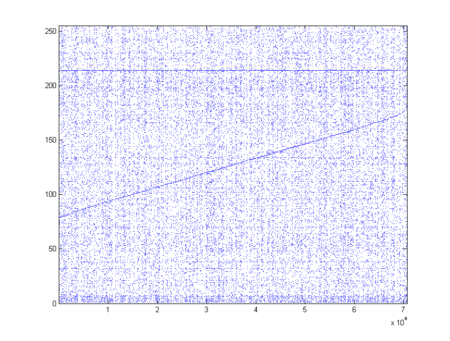
The DCS/2 experiment is a re transmission from mobile platforms (sea buoys, arctic fox collars, sea ice monitors, weather balloons etc etc). The format is not provided, as the instrument is owned and managed by CNES of France. I plotted the raw stream to tease out patterns in the data. What juicy mysteries lay here :)
Interestingly enough, the DCS/2 experiment locks onto the mobile transmitter and records the frequency deviation. Using this data and knowing the orbit of the satellite, it is possible to calculate the location of the mobile platform by using its Doppler shift... Even if we can only take guesses at what it may be, it should be possible to plot these locations on a map if we can just find the right data...
Looking at this plot, it is easy to see that there are two very clear trends. There is the value 214 (0xD6 or 11010110) that appears over and over again and there is also what looks like a linearly increasing value, perhaps a counter or clock. Looking at the data, a lot of instances of 0xD6 are preceeding by lots and lots of zeros. This must be the message start sync word! Searching for "00 00 D6" (which probably excludes packets that are closely spaced, but captures most of them) and grabbing the following 64 bytes (surely enough bytes to see any patterns in the data) yields a long dist of messages, some of which are longer than 64 bytes and some that are very small. All are at least 9 bytes long, and have several fixed values (which may be dynamic between spacecraft or data-sets, remember, this is only one NOAA-15 pass we are looking at)
An example of the messages follows (the entire list can be found here http://nebarnix.com/sdr/DCS_64B.txt): Actually here's a better example with the packets trimmed to avoid duplicates and trailing zeros. http://nebarnix.com/sdr/DCS_6_Europe_64B.txt
D6 01 CB A6 77 74 CF 18 30 00 3A 62 D0 82 E2 F4 C4 3A 15 C1 57 47 04 AE 45 44 41 70 23 8E 08 E3 B1 C8 E4 71 40 9C 31 94 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 D6 04 FA 46 77 7E 68 D6 04 FA 46 77 7E 68 88 B0 E1 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 92 9D 8B 00 00 00 00 00 00 00 00 00 00 D6 01 22 46 77 CA 8F 9E A0 8B 40 D6 01 22 46 77 CA 8F 9E A0 8B 40 00 00 C4 E8 2F 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 D6 01 0A 26 78 14 D5 92 00 BE B7 C8 B9 B5 E8 29 00 00 00 00 00 00 D6 06 C3 06 77 EB B7 D9 80 AD 35 4D BE CD BE F5 A2 C3 B9 CB BB 7C 53 C1 21 6D D8 F7 D1 55 F5 AD 3F B0 59 C7 79 84 A6 84 D6 00 A3 D6 06 C3 06 77 EB B7 D9 80 AD 35 4D BE CD BE F5 A2 C3 B9 CB BB 7C 53 C1 21 6D D8 F7 D1 55 F5 AD 3F B0 59 C7 79 84 A6 84 D6 00 A3 A6 77 F5 66 3D E0 4C 10 11 F1 CB 78 63 D6 63 D4 DD 39 FC 6E AC D6 D6 02 09 86 78 63 C0 AF D0 02 97 29 BC 96 2A BF 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 D6 D6 06 F3 66 78 48 6D 9E 60 35 E3 00 00 00 00 00 00 03 00 1B 34 00 00 00 00 00 00 32 01 B3 80 00 00 00 00 00 03 20 1B A0 91 A0 0E 6B 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 D6 01 6A A6 78 84 69 44 60 6A 84 12 41 AC B5 DE B2 7D A7 B5 F1 E4 85 CB 5D 81 13 83 D6 00 C4 A6 78 6C CE F7 00 F2 34 A1 4A FA E1 18 90 32 15 72 5C 85 C8 B9 04 57 45 70 00 00 00 00 00 00 00 01 20 D6 06 C4 26 78 B8 B7 0F 60 79 36 E1 F6 E5 48 BE D9 76 6E F7 19 7B FB 48 39 45 6B 44 FB D7 14 FF 6D 66 B1 E4 FF 47 03 AA D6 00 C5 C6 78 86 22 A3 50 35 3D 46 C4 2B 02 A8 66 5C C4 DC 38 66 71 5E EC D6 01 FB 06 78 CF D8 62 70 AD DF 14 2E 02 88 03 92 57 71 93 81 7B 2B A7 AF 73 3B F3 8B B5 FB BB BF BB BE FF FB FF FF FF FC C1 FD 0F D6 03 C1 86 78 E2 B6 B3 50 D4 3C 03 47 BF 96 EC 20 D0 A5 A5 C9 D6 02 CA 46 78 FA B7 47 F0 F2 3F 6E C1 3C EC 17 34 06 02 F7 74 39 DC 85 97 B8 66 29 E7 FF 7F 80 77 F0 1E 69 82 63 88 81 D6 04 CD 86 79 01 90 63 50 F2 3A 00 D3 81 17 2E B4 52 BF 3A 23 99 CC B1 B5
Updated list with better processing and line numbers
1110: D6 05 03 77 0E 0E D6 4C 60 C7 AD C0 C0 B4 13 32 1111: D6 03 C5 17 0E 01 B8 03 30 5F 39 CF 10 B3 EB 01 D6 F0 82 DE 37 A1 73 5A E3 C9 0C E1 75 78 A9 FA E7 70 07 70 5E 55 BF 67 1112: D6 00 93 97 0E 15 5D 93 80 AD D8 B5 F7 C6 AD 42 84 F3 C6 0A 5D D8 00 7F 4E C1 FF FA 00 83 DA 0C 1113: D6 02 3A F7 0E 2F B8 03 30 00 FF 80 E8 26 B8 03 B8 A9 F0 90 1114: D6 04 AE 57 0E 1F 69 DF 20 4C 08 12 61 C2 89 DD B6 28 4A A0 7C E8 E9 D3 95 56 8B 25 27 83 FB 81 7B 6C 5D E3 1115: D6 05 C3 77 0E 34 2F 64 00 BE 36 DD 5A A1 BE 0A D7 9B 9F 65 BA 94 8D E5 52 19 F8 EA DB 6E D8 59 0C 84 7E 1A 6A 35 88 C0 1116: D6 00 04 17 0E 7C D4 33 80 00 00 00 00 87 DE 28 1117: D6 01 CD B7 0E 8F 9F B6 B0 6A 30 F9 BE 1D AC 69 FB 69 FB 91 87 57 E4 79 F3 BC AE B4 A8 80 E7 06 82 C4 C3 33 57 C0 03 F9 1118: D6 07 CB B7 0E 9B D3 DA 60 8B 3A 4C AA B5 D1 17 D2 BE 15 72 5C 85 C8 B9 04 57 45 70 00 00 00 00 00 00 00 01 40 9D 95 40 1119: D6 02 CB 97 0E A7 B6 DD 10 BE 32 F3 22 C9 12 49 2D 2C 67 C8 DD C5 51 89 0B B5 6F 73 C1 3A F3 7E 36 D5 14 FA 2C 76 A1 4D 1120: D6 03 F2 B7 0E A7 07 D7 B0 D4 92 8B 1B 5B 98 30 A9 33 79 FB 86 49 8E 71 69 B0 CA 36 CE CC 94 17 8E 41 D9 92 C2 F1 C8 BE B5 AB 82 F8
Analysis of data
Now an interesting thing happens if we move this data to a spreadsheet and create a field to calculate packet length then sort by it. We can possibly assume that some/most/all transmitters will transmit the same packet structure each time, which means the same length of packet.
These are the 28 byte long packets. There are a lot of them, but if we start to look at the structure some details emerge. Look at the columns and suddenly "E1 E6 D0" pops out more than once. So does "67 8E 80 00"
22 28 D6 05 61 D6 9F 04 69 59 D0 0C EE CF 68 76 48 8B 55 3C 51 4A 85 64 51 4A 25 7C CD 22 28 28 D6 00 62 B6 9F F7 25 49 A0 8B A0 54 96 C5 D3 A3 DD 67 D2 22 98 A6 25 49 25 46 02 FA 153 28 D6 00 64 16 AA C2 22 9B 20 8B AE 5F 4F C2 7D D0 88 CC 8C D8 89 91 91 0B 36 45 8F AF 282 28 D6 03 66 76 B8 A7 69 44 60 6A 84 12 41 A0 DB EF D2 7D A7 B5 F6 2B AD B4 A2 89 A0 C8 354 28 D6 03 64 16 BE 20 **67 **8E **80 **00 2F 12 14 A1 CB DD 6C 55 8B 32 2C F1 D5 97 1A 98 9F 73 516 28 D6 02 6A B6 D4 D0 *E1 *E6 *D0 *BE A3 E0 F7 9F 80 0E EE C0 0E E2 00 3F 57 40 8F BD 73 94 568 28 D6 06 62 16 D8 6B CF A5 A0 26 A3 60 12 1E 01 0E 00 27 09 F4 5F FF FF FF 3E BF 90 F4 585 28 D6 00 64 B6 D9 D8 B6 D5 70 C7 A9 75 EF 3B E8 DE B9 7A 4E 1A 23 A2 B6 D7 B6 BA 37 FC 617 28 D6 07 6D F6 DC A5 69 44 60 6A 84 12 41 A0 13 EF F2 7D A7 B5 F6 2B B5 B4 A2 83 13 FC 681 28 D6 07 6D 36 E2 F1 **67 **8E **80 **00 2F 12 14 A5 CB DD 6C 55 8B 36 2C F1 EC F7 16 90 E7 B1 686 28 D6 07 6A F6 E3 48 CE E5 A0 12 23 C2 FF F2 E1 00 00 EE 00 0E 0E E5 FF F9 E4 BD 55 6C 765 28 D6 07 6A 56 EA 0F 25 49 A0 8B A0 54 96 C5 53 A3 DD 67 D2 22 98 A4 25 49 25 3C E2 5A 853 28 D6 06 F2 B6 F1 AA F1 19 B0 8B 96 4B 0E 06 C7 00 B0 F1 21 4A 80 00 00 00 00 86 50 4C 936 28 D6 05 63 16 FC 49 D0 A7 30 C7 42 72 01 59 6C 24 B0 1C 40 00 00 00 00 56 00 58 DA A0 989 28 D6 00 63 97 01 75 69 44 60 6A 84 12 41 A5 83 EE 52 7D A7 B5 F6 2B 85 B4 A2 80 D9 95 1047 28 D6 03 65 97 07 C1 **67 **8E **80 **00 2F 12 14 AD CB DD 6C 55 8B 38 2C F1 D2 D7 11 8C 24 B0 1103 28 D6 07 6C D7 0D A1 81 BA D0 96 D6 1F 3E 00 17 00 1C 88 C0 00 00 00 1D 0E 60 90 5D AB 1109 28 D6 07 6D 97 0D DF 9F AD 20 98 A1 8A 12 52 4D 58 BA D3 69 52 8D 7D 9F AD 9F 80 DC 44 1170 28 D6 07 6B 37 13 16 D0 A7 30 C7 42 72 01 59 6C 24 B0 1C 40 00 00 00 00 56 00 57 6D 44 1212 28 D6 04 6A 77 16 80 B7 2C 80 D4 A9 D9 96 57 CD C2 69 1A 6C 40 38 4B 95 3D 36 59 8C A4 1260 28 D6 00 63 B7 1B 41 01 FB F0 79 8F AB DA 64 94 F3 48 78 C3 3F 02 01 00 00 00 A4 46 8E 1346 28 D6 04 6A B7 22 F5 CE 16 C0 79 E6 02 4C BA 59 DC F2 11 EF 37 03 AD 89 48 00 7F 1B A1 1386 28 D6 03 62 F7 26 46 69 44 60 6A 84 12 41 A0 FB EF 22 7D A7 B5 F6 2B 8D B4 A2 80 13 BE 1392 28 D6 05 66 77 26 A7 B6 D7 70 C7 A8 B5 EF 7B FE 5E B9 62 4E 08 22 E2 B6 D7 B6 AC B8 03 1406 28 D6 04 6C 17 27 F5 *E1 *E6 *D0 *BE A4 20 FF FF 1E 0E 00 10 0E E0 00 00 EE 00 26 A6 97 FD 1409 28 D6 00 63 37 28 47 CE 19 90 26 DC 02 4C BA 59 E6 F5 11 E9 B7 EE 30 89 48 00 7E 9D D5 1461 28 D6 06 64 D7 2C 92 **67 **8E **80 **00 2F 12 14 A1 CB DD 6C 55 8B 3C 2C F1 D0 37 00 89 C9 79
If we sort on these presumed transmitter ID bytes we can assume that we have isolated individual data sets spanning the 400 seconds that the satellite was overhead. Two such transmitters in this data set are shown below
354 28 D6 03 64 16 BE 20 67 8E 80 00 2F 12 14 A1 CB DD 6C 55 8B 32 2C F1 D5 97 1A 98 9F 73 681 28 D6 07 6D 36 E2 F1 67 8E 80 00 2F 12 14 A5 CB DD 6C 55 8B 36 2C F1 EC F7 16 90 E7 B1 1047 28 D6 03 65 97 07 C1 67 8E 80 00 2F 12 14 AD CB DD 6C 55 8B 38 2C F1 D2 D7 11 8C 24 B0 1461 28 D6 06 64 D7 2C 92 67 8E 80 00 2F 12 14 A1 CB DD 6C 55 8B 3C 2C F1 D0 37 00 89 C9 79 282 28 D6 03 66 76 B8 A7 69 44 60 6A 84 12 41 A0 DB EF D2 7D A7 B5 F6 2B AD B4 A2 89 A0 C8 617 28 D6 07 6D F6 DC A5 69 44 60 6A 84 12 41 A0 13 EF F2 7D A7 B5 F6 2B B5 B4 A2 83 13 FC 989 28 D6 00 63 97 01 75 69 44 60 6A 84 12 41 A5 83 EE 52 7D A7 B5 F6 2B 85 B4 A2 80 D9 95 1386 28 D6 03 62 F7 26 46 69 44 60 6A 84 12 41 A0 FB EF 22 7D A7 B5 F6 2B 8D B4 A2 80 13 BE
One can see that large bits of data did not change, perhaps several hundred seconds is not enough time for the parameter to experience disruption.
Further Analysis
Byte 1 Always 214 (0xD6)
Byte 2 Upper nibble always 0, Lower nibble 0-7, perhaps the sat receiver channel? We know from data sheets there are 8 channels
Byte 3 Upper nibble is related to packet length, which is between 4 and 32 bytes in 4 byte increments not including the header and suffix
Byte 4 Contains 0-7 channels in the upper 3 bytes the lower 5 bits contain the upper nibble+ of the counter (rollover behavior into this byte was observed)
Byte 5 Middle byte of timestamp
Byte 6 lower byte of timestamp - granularity 1/100th of a second
Byte 7 contains embedded trends
Byte 8 Likely to be the transmitter ID byte 1
Byte 9 Contains 0-16 in the upper nibble with 0's in the lower nibble -- I believe this is the transmitter ID byte 2
Byte 10 Likely to be the transmitter ID byte 3
Byte 11 Likely to be the transmitter ID byte 4
The last three bytes are always dynamic. Looks like some data is appended to them.
Byte N-2 This is *always* seen to be descending among ID groups with time. Assume that this is the doppler shift
Byte N-1 Unsure. Perhaps RSSI?
Byte N Also could be RSSI, also could be 2 values split into 2 12-bit numbers. Also CRC? CRC16?
Orbital Determination
In order to correlate the doppler shifts to geo-locations we need to know the position of the spacecraft at each moment. Matlab does not have readily available tools to do this, so I wrote a quick python script using pyephem. Its quick, dirty, and a very rough draft.
#!/usr/bin/env python
#NOAA 15
#1 25338U 98030A 15273.50150732 .00000073 00000-0 49665-4 0 9996
#2 25338 98.7779 272.2357 0009845 218.3502 141.6978 14.25663704903843
import ephem
line1 = "NOAA-15"
line2 = "1 25338U 98030A 15273.50150732 .00000073 00000-0 49665-4 0 9996"
line3 = "2 25338 98.7779 272.2357 0009845 218.3502 141.6978 14.25663704903843"
NOAA15 = ephem.readtle(line1, line2, line3)
NOAA15.compute('2015/9/6 15:38:58.685')
#NOAA15.compute('2015/9/6 15:33:6.685')
#NOAA15.compute('2015/9/6')
print('%s %s' % (NOAA15.sublat, NOAA15.sublong))
The (painfully manually entered dates and times) come out as latitudes and longitudes looks like this when you replace the :'s with degrees and minutes symbols, which corresponds to the major frame times which I added manually. Between these points, a linear interpolation will suffice for a first cut at plotting DCS idents.
Local Seconds Lat Lon 046.6725 43°21'31.6 21°17'02.6 078.6725 45°12'57.1 20°35'2.8 142.6755 48°55'13.7 19°03'51.1 174.6755 50°46'1.6 18°13'57.4 206.6755 52°36'33 17°20'37.5 238.6755 54°26'45.4 16°23'19.0 270.6755 56°16'35.8 15°21'23.1 302.6755 58°06'0.1 14°14'2.5 334.6755 59°54'53.8 13°00'19.1 366.6755 61:43:10.7 11:39:1.0 398.6755 63:30:43.6 10:08:37.7
Todo
- Finish HIRS data extraction (holy crap there is a lot of different data sets in there!)
- Maybe port this matlab script into sci-py and integrate directly into GNU radio block for realtime plotting and processing etc
- Finish figuring out the DCS/2 mystery and even make a plot on a map of the transmitters.